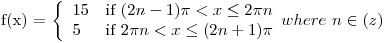Discrete vs Continous
There are two types of phenomina: discrete and continuous. Someting that is continous can hold an infinite number of itermediate values. An example is the angle a swinging pendulum makes. Something that is decrete can only hold a finite number of states and changes values in steps. An example of this would be the number of people sitting at a table. There could be 0, 1, 2, 3, ect ... people at a table, but no fractional numbers of people. This means that the number of people can only change in whole units.
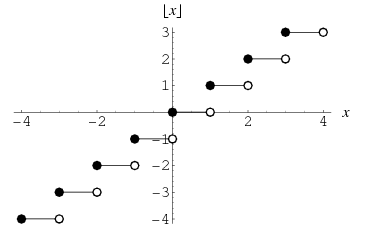
Graph of the greatest interger function
Graph of the sine function
Storing Numbers
The larger the number the more space it takes up whether on paper, in a computer's random access memory, or any other storage medium. A number n takes up ceil(log(n)) digits of space. Ceil is the ceiling function which rounds a number up the nearest interger. Thus, 2014 takes ceil(log(2014)) = ceil(3.304...) = 4 digits. Other bases can be used. One of the most common is binary (base 2). In binary the decimal number 5 would be written as 101 because 1*2^2 + 0*2^1 + 1*2^0 = 5. Base two is used by computers because a piece of memory can only have two states: on or off. The space a piece of data takes up is measured in bits which stands for binary digits. Because a bit is a very small unit, people tend to use bytes instead (a byte is 8 bits and can hold 2^8 = 256 different values.
Quantization
The frequency of a sound wave could be represented by a continuous function. If an attempt were made to store the frequency of a sound wave how many bits (space) would be needed? If complete accuracy were to be obtained, infitely small subdivisions would have too be used and and infinite number of digits would be needed. To solve this problem the value is rounded to a certain persision. By doing this, the continous function representing the frequency is made discontinuous. This process is called quantization and allows for a value to be stored with a specifiable number of bits at the expence of some precision. If f(x) is continous over the range a <= f(x) <= b the range of the function can be made into a finite set of discrete values rather than an infinite number of continous ones. A quantization function q(x) = round(f(x)/Q), where Q is the quantization factor and there are round((b - a)/Q) steps of equal size, can be created to make the range of a given function discrete rather than continous. The greater the value of Q, the fewer steps there are, which means that fewer bits are needed to store the function's output.
Fourier Series
Fourier Series are used to approximate a function using a series of sine and cosine functions in the form an(x) = a0 + a1sin(x) + b1cos(x) + a2sin(2x) + b2cos(2x) + a3sin(3x) + b3cos(3x) + ... + ansin(nx) + bncos(nx). How accurate an approximation of a function is depends on the criteria being used to evaluate accuracy. Some approximations might give the right extrema, but the wrong concavity, while others might do the opposite. The measure of accuracy that Fourier Series are based off of, at is the area under the curve.
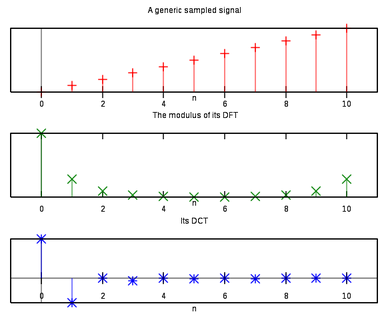
In a Fouries series of f(x), the following conditions must hold true.
![[tex]$$\int_{0}^{2\pi} a_n(x) dx = \int_{0}^{2\pi} f(x) dx$$[/tex]](fourierCondition1.gif)
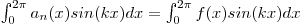
and
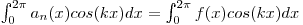
where
k = 1,2, ... n
These restrains allow the coefitients for the series to be determined.
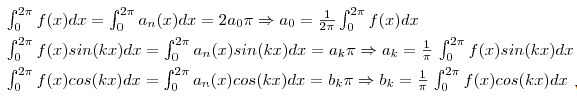
where
k = 1,2,...n
Integrals can always be approximated with Reiman Sums or the trapezoid, so the coefitients can be determined for any function that is defined for all points on an interval. If the desired interval is not [o,2π] and is instead [a,b], the substitution t = 2π(x - a)/(b - a) can be used to write a new series in terms of t.
A Fourier Seriers is defined over the range of all real numbers and is periodic. Because it is periodic, it is used to approximate periodic function. When the function is to be approximated only on a single nonrepeating interval, a Fourier Transform which used exponentials as its basic building blocks could be used. The transform that is used most in image compression is the Discrete Cosine Transform, which approximates a function on a finite interval (like the Fourier Transform), but using cosines instead. The reason the Discrete Cosine Transform is used is because it is very energy compact, meaning that only a small number of coefitients are needed.
The graphs above compare the DCT with the DFT. The DCT (the bottom graph) steadily decreases in value. This means that each additional coefitient does less error correcting than the previous coefitients and that the first few coefitients do most of the work of approximating and the following could often be discared. This property of energy compactness is why the DCT is used in compression algorithms.
Images and Image Gradients
Images tend to be stored as a matrix of pixels where each pixel has a Red, Green, and Blue component. Some images have a transparency component in addition. One of the many properties an image has is its gradient. The gradient of an image shows how much the value of one pixel differs from the ones next to it. In most photographs there is little difference between adjecent pixels.
JPEG
JPEG image compression uses the DCT and quantization to store an image using fewer bits. The algorithms is lossy, which means that some of the original information is lost. Because of the energy compactness of the Discrete Cosine Transform, the information loss is minimal and any differences are unlikely to be precieved. Lots of other tricks are used to trick our vision into not noticing the slight differences between the new and original image.
Each of the pixels that JPEG algorithm operates have 8-bits for the Red, Green, and Blue portions. This means that each color can hold values from 0 to 255. These values are shifted to be -128 through 127 for processing because the Discrete Cosine Transform uses cosines whose ranges are half negative and half positive values.
Steps
- The image is broken into 8 by 8 blocks (the number is arbitrary). If the image's dimensions are not divisible by 8, the image is padded.
- For each of the blocks the Discrete Cosine Transform of the image is calculated.
- The coefitients of obtain are run through a quantizing function (this is where loss of information occurs)
- The output of the previous step has lots of repitition and is sent throught an entropy encoder that uses run length encoding and huffman encoding to produces the final compessed product.
- Some metadata is then tacked on that identifies the file format and alogorithm used


![[tex]$$\int_{0}^{2\pi} a_n(x) dx = \int_{0}^{2\pi} f(x) dx$$[/tex]](fourierCondition1.gif)
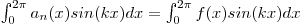 and
and
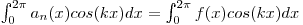 where
where